The Laplace transform is 1 s but the imaginary axis is not in the ROC and therefore the Fourier transform is not 1 jω in fact the integral f t e jωt dt 0 e jωt dt 0 cos ωtdt j 0 sin ωtdt is not defined The Fourier transform 119. The Fourier transform is an integral transform widely used in physics and engineering.

What Is A Fourier Transform It Decomposes A Function Of Time A Signal Into Its Constituent Frequencies This Is Simila Solving Equations Math Tutor Calculus
Fω 1 2π Z dtfteiωt 11 3 Example As an example let us compute the Fourier transform of the position of an underdamped oscil-lator.

. Xxxiv and and are sometimes also used to. Imagine playing a chord on a piano. If a sine wave decays in amplitude there is a smear around the single frequency.
An animated introduction to the Fourier TransformHelp fund future projects. The Fourier transform FT decomposes a function of time a signal into the frequencies that make it up in a way similar to how a musical chord can be expressed as the frequencies or pitches of its constituent notes. The Fourier transform is applied to waveforms which are basically a function of time space or some other variable.
Fourier transform has many applications in physics and engineering such as analysis of LTI systems RADAR astronomy signal processing etc. Ad Find the right instructor for you. Fourier transform is a mathematical transform that decomposes functions depending on space or time into functions depending on spatial or temporal frequency such as the expression of a musical chord in terms of the volumes and frequencies of its constituent notes.
The Fourier transform The Fourier transform maps a function to a set of complex numbers representing sinusoidal coefficients We also say it maps the function from real space to Fourier space or frequency space Note that in a computer we can represent a function as. Consider a periodic signal ft with period T. They are used in processing many of the signals we encounter in our everyday lives such as phone and TV signals and even in the evolution of the Stock Market.
They are widely used in signal analysis and are well-equipped to solve certain partial differential equations. A Fourier Transform of a sine wave produces a single amplitude value with corresponding phase not pictured at a single frequency. Fourier transforms break down signals into oscillations that persist over the entire sequence.
A fast Fourier transform FFT is an algorithm that computes the discrete Fourier transform DFT of a sequence or its inverse IDFT. The Fourier transform is called the frequency domain representation of the original signal. The Fourier transform is a generalization of the complex Fourier series in the limit as.
Its inverse is known as Inverse Discrete Fourier Transform IDFT. The Fourier transform of a function of x gives a function of k where k is the wavenumber. A discrete Fourier analysis of a sum of cosine waves at 10 20 30 40 and 50 Hz.
The term Fourier transform refers to both the frequency domain representation. The notation is introduced in Trott 2004 p. Deriving Fourier transform from Fourier series.
Wavelet Transform vs. Today Fourier transforms are prevalent in many areas of science and engineering. The Fourier transform of a function of t gives a function of ω where ω is the angular frequency.
The convergence criteria of the Fourier transform namely that the function be absolutely integrable on the real line are quite severe due to the. When played the sounds of the notes of the chord mix together and form a sound wave. What is the Fourier transform of f t 0 t 0 1 t 0.
The discrete Fourier transform is an invertible linear transformation. With denoting the set of complex numbers. It is a way of taking a signal or a function and deconstructing it into a series of sines and cosines.
The quicker the decay of the sine wave the wider the smear. Choose from many topics skill levels and languages. In other words for any an N -dimensional complex vector has a DFT and an IDFT which are in turn -dimensional complex vectors.
The Fourier transform is a mathematical function that takes a time-based pattern as input and determines the overall cycle offset rotation speed and strength for every possible cycle in the given pattern. Fourier transforms is an extremely powerful mathematical tool that allows you to view your signals in a different domain inside which several difficult problems become very simple to analyze. Then change the sum to an integral and the equations become.
Wavelet transforms perform a similar function however they can break signals down into oscillations localized in space and time. Join millions of learners from around the world already learning on Udemy. Replace the discrete with the continuous while letting.
This works because each of the different notes waves interfere with each other by adding together or. The Fourier transform is a mathematical function that can be used to find the base frequencies that a wave is made of. Fourier analysis converts a signal from its original domain often time or space to a representation in the frequency domain.
Is called the inverse Fourier transform. Therefore the Fourier transform of cosine wave function is F c o s ω 0 t π δ ω ω 0 δ ω ω 0 Or it can also be represented as c o s ω 0 t F T π δ ω ω 0 δ ω ω 0 The graphical representation of the cosine wave signal with its magnitude and phase spectra is shown in Figure-2.
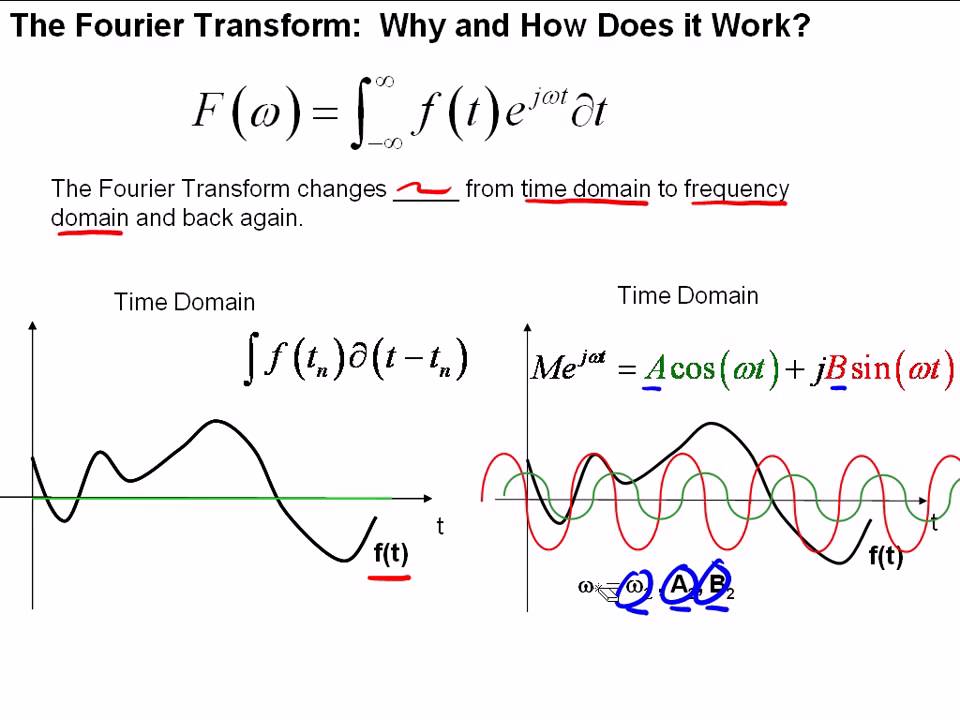
The Fourier Transform Part I Youtube Learning Mathematics Math Quotes Studying Math

Z Transform Fourier Transform Z Transform Z Transform Operator The Z Transform Operator Is Seen To Transf Laplace Transform Signal Processing Transformations

Pic 1 Fourier Series We Have Learnt A Bit About The Needed Basics Before Beginning The Fourier Series And The Euler S Formu Math Poster Cymatics Triangle Wave

Demystifying The Fourier Transform Discrete Fourier Transform Exponential Functions Complex Plane

Short Time Fourier Transform Matlab Stft Discrete Fourier Transform Signal Processing Math Methods

Fourier Transform Table Stamp Free Math Resources Transformations Free Math

Fourier Transform Google Search Math Methods Learning Math Mental Math

Fourier Transform Transformations Graphing Physics

But What Is The Fourier Transform A Visual Introduction Youtube Electrical Engineering Transformations Engineering

Prove This Fourier Transform Table From Physics And Mathematics Learning Mathematics Calculus

Fourier Transform Table Outline Math Measurement Physics And Mathematics Math Methods

The Fourier Transform Is A Mathematical Technique That Allows An Mr Signal To Be Decomposed In Fourier Transformation Physics And Mathematics Laplace Transform

Fourier Transform Google Search Physics And Mathematics Math Methods Math Geometry

Coherent Transfer Function Fourier Transforms Transfer Function Wave Function Physics And Mathematics

Brilliant Fourier Transform Tutorial Transformations Tutorial Science And Technology

Fourier Transform Table Dress Calculus Textbook Physics Classroom Maths Algebra

The Fourier Transform Is A Mathematical Technique That Allows An Mr Signal To Be Decomposed Into A Sum Of Physics And Mathematics Maths In Nature Math Formulas

Fourier Transform Table Draft Fourier Transformation Mathematics Laplace

